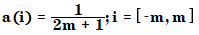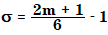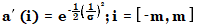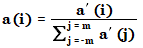Algorithm details

Moving average

The Moving average is the simplest smoothing algorithm. All coefficients are computed as follows:

where
a	Array of smoothing coefficients
m	Even number specifying the half width of the smoothing window

This means the smoothing function has a rectangular shape. This kind of smoothing is also called boxcar averaging.

Gaussian

Gaussian smoothing uses coefficients sampled from the Gauss normal distribution. Given the number 2m+1 as window size, the standard deviation σ of the normal distribution is computed as follows:

The individual coefficients are then computed as:

In a second step the coefficients are normalized such that the sum is 1:

Savitzky-Golay

The coefficients for Savitzky-Golay smoothing are computed in a way that ensures that the area under the function remains unchanged. The computation of coefficients is based on the paper General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method by Gorry (1990) * * Gorry, P.A., 1990. General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method. Analytical Chemistry 62, 570-573..

This computation makes sure that the area-preserving properties of the Savitzky-Golay smoothing are also valid at the borders of the signal.