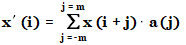General approach

Assumptions

All smoothing algorithms assume that the data is equidistant data. Non-equidistant data is transformed into equidistant data by applying an interpolation and resampling the data using the smallest time difference in the non-equidistant data.

Non-MS data is transformed using spline interpolation.

For MS data, the transformation depends on the smoothing algorithm. With Savitzy-Golay, spline interpolation is used. With Moving average or Gaussian, linear interpolation is used.

Smoothing - base algorithm

All smoothing algorithms apply a window of size 2m+1 populated with smoothing coefficients, using the following approach:

where
a	Array of smoothing coefficients
x'	Smoothed signal
m	Even number specifying the half width of the smoothing window

This approach leads to an odd number 2m+1 for the total window size.

Handling the edges

Since the smoothing coefficients are supposed to be normalized, the edges need special consideration.

For Moving average and Gaussian filtering, the window is pruned at the left or right edge, and the coefficients are recomputed to have a total sum of 1 (normalization).

For Savitzy-Golay the handling is more complicated. It needs to preserve the properties of Savitzky-Golay filtering also close to the edges of the signal. See Algorithm details.