Calibration curve statistics

The calibration curve calculation provides for each curve the correlation coefficient, coefficient of determination and residual standard deviation figures.

Correlation Coefficient

The correlation coefficient (r) gives a measure of the fit of the calibration curve between the data points. It is calculated using the following equation:

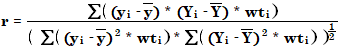
where

	r	Correlation coefficient
	wt_i	Weight of the data point
	ӯ	Mean values of the measured responses or amounts If the calibration curve is forced through the origin (Origin=Force in the processing method), OpenLab CDS calculates the uncentered determination coefficient. In this case, ӯ is omitted.
	yi	Measured response (Area, AreaRatio (ISTD method), Height or HeightRatio (ISTD method)) or amount (Amount, AmountRatio (ISTD Method)), depending on calibration mode
		Mean values of the predicted responses or amounts
	Yi	Predicted response or amount (using the calibration curve)

and are mean values of the measured and predicted responses or amounts, calculated as follows:

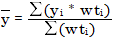
where

	wt_i	Weight of the data point
		Mean values of the measured responses or amounts
	yi	Measured response (Area, AreaRatio (ISTD method), Height or HeightRatio (ISTD method)) or amount (Amount, AmountRatio (ISTD Method)), depending on calibration mode

and

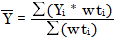
where

	wt_i	Weight of the data point
		Mean values of the predicted responses or amounts
	Yi	Predicted response or amount (using the calibration curve)

For Forced Origin it is assumed that the points are centered on zero (mirrored to third quadrant) and the mean values are substituted with zero. 3rd party calculation programs may use a different approach, which will lead to slightly different results.

The correlation coefficient is 1 for a perfect fit. It reduces as the individual or averaged calibration points deviate from the regression curve. Typical values are between 0.99 and 1. The correlation coefficient is not a direct measure for precision of the analytical method, but low values indicate low precision.

Determination coefficient

The determination coefficient (R²) is calculated as follows:

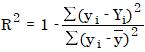
where

	R2	Determination coefficient
		Mean values of the measured responses or amounts If the calibration curve is forced through the origin (Origin=Force in the processing method), OpenLab CDS calculates the uncentered determination coefficient. In this case, ӯ is omitted.
	yi	Measured response or amount. Response can be area (Area, Area%, or AreaRatio (ISTD method)) or height (Height, Height%, or HeightRatio (ISTD method)). Amount can be absolute amount or AmountRatio (ISTD method). The type of value depends on the calibration mode.
	Yi	Predicted response or amount (using the calibration curve)

Residual standard deviation

The residual standard deviation (sometimes referred to as the root mean square error) is calculated using the following formula:

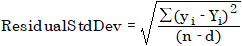
where
d = 3	Degree of freedom for a quadratic curve, no forced origin
d = 2	Degree of freedom for a quadratic curve with forced origin, or Degree of freedom for a linear curve, no forced origin
d = 1	Degree of freedom for a linear curve with forced origin
ResidualStdDev	Residual standard deviation
yi	Measured response (Area, AreaRatio (ISTD method), Height or HeightRatio (ISTD method)) or amount (Amount, AmountRatio (ISTD Method)), depending on calibration mode
Yi	Predicted response or amount (using the calibration curve)
n	number of calibration points

For Include origin calibration curve types, the origin (0,0) is included as a regular point in the calculation and counted by n.

The y values are not weighted.

The residual standard deviation gives a more sensitive measure of the curve quality than does the correlation coefficient. For a perfect fit, the residual standard deviation is zero. With increasing residual standard deviation values, the calibration points get further away from the curve.

Standard deviation

The standard deviation is calculated with the formula for the population standard deviation:

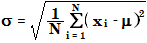
where
σ	Standard deviation
N	Number of samples
x_i	Measured value response or amount. For the curve model Average RF, it is the response factor RF of a compound in a single sample.
μ	Mean value. For the curve model Average RF, it is the average response factor of a compound in all samples.

For the curve model Average RF: Due to the normally rather small population (number of calibration points), this formula is used instead of the sample population standard deviation (with N-1 as denominator).

Relative standard deviation

The relative standard deviation is calculated as follows:

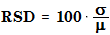
where
RSD	Relative standard deviation
σ	Standard deviation
μ	Mean value

PVCS#B-02561