アルゴリズムの詳細

移動平均

移動平均は、最も単純なスムージングアルゴリズムです。係数は以下のように計算されます。

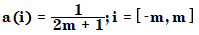
場所

a	スムージング係数の配列
m	スムージングウィンドウの半値幅を指定する偶数

したがって、スムージング関数は矩形を有しています。この種類のスムージングは Boxcar averaging とも呼ばれます。

ガウス

ガウススムージングは、ガウス正規分布からサンプリングされた係数を使用します。数値 2m+1 をウィンドウサイズとすると、正規分布の標準偏差 σ が以下のように計算されます。

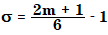
次に、個々の係数が以下のように計算されます。

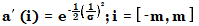
2 番目のステップで、係数は合計が 1 になるようにノーマライズされます。

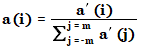
Savitzky-Golay

Savitzky-Golay スムージングの係数は、関数の下の面積が変わらないように計算されます。係数の計算は、Gorry による論文『General Least-SquaresSmoothing and Differentiation by the Convolution (Savitzky-Golay) Method』（1990）Gorry, P.A., 1990. General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method. Analytical Chemistry 62, 570-573. に基づいています。

この計算により、Savitzky-Golay スムージングで面積が維持される特性がシグナルの境界でも有効になります。