알고리즘 세부 정보

이동 평균

이동 평균은 가장 간단한 평활화 알고리즘입니다. 모든 계수는 다음과 같이 계산됩니다.

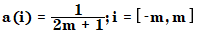
위치

a	평활 계수의 배열
m	평활화 창의 절반 너비를 지정하는 짝수

즉, 평활화 함수는 직사각형 형태를 갖습니다. 이러한 종류의 평활화를 박스카 평균화라고도 합니다.

가우시안

가우시안 평활화는 가우스 정규 분포에서 샘플링된 계수를 사용합니다. 창 크기로 2m+1라는 숫자가 주어지면 정규 분포의 표준 편차 σ는 다음과 같이 계산됩니다.

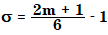
그런 다음 개별 계수는 다음과 같이 계산됩니다.

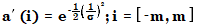
두 번째 단계에서는 계수의 합이 1이 되도록 계수를 정규화합니다.

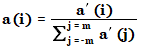
Savitzky-Golay

Savitzky-Golay 평활화 계수는 함수 아래 면적이 변하지 않도록 하는 방식으로 계산됩니다. 계수 계산은 General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method by Gorry (1990) ToDo: Footnote "Gorry, P.A., 1990. General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method. Analytical Chemistry 62, 570-573" 논문에 기반합니다. .

이 계산은 Savitzky-Golay 평활화의 면적 보존 특성이 신호의 경계에서도 유효한지 확인합니다.