결합된 검량 곡선 통계
결합된 검량 곡선 계산은 각 곡선에 대해 상관 계수, 결정 계수 및 잔차 표준 편차 수치를 제공합니다.
상관 계수
상관 계수(r)는 데이터 포인트 간의 결합된 검량 곡선 피팅을 측정합니다. 다음 공식을 사용하여 계산됩니다.
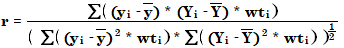
여기에서
| r | 상관 계수 |
| wti | 데이터 포인트의 가중치 |
| ӯ | 측정된 감응 또는 양의 평균 값 결합된 검량 곡선이 원점을 강제로 통과하는 경우(처리 방법에서 원점=힘) OpenLab CDS는 중심이 없는 결정 계수를 계산합니다. 이 경우 ӯ는 생략됩니다. |
| yi | 검량 모드에 따라 측정된 감응(면적, 면적 비율(ISTD 분석법), 높이 또는 높이 비율(ISTD 분석법)) 또는 양(양, 양 비율(ISTD 분석법)) |
| Ȳ | 예측된 감응 또는 양의 평균 값 |
| Yi | 예측된 감응 또는 양(결합된 검량 곡선 사용) |
ȳ 및 Ȳ는 측정 및 예측된 감응 또는 양의 평균값으로 다음과 같이 계산됩니다.
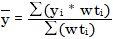
여기에서
| wti | 데이터 포인트의 가중치 |
| ȳ | 측정된 감응 또는 양의 평균 값 |
| yi | 검량 모드에 따라 측정된 감응(면적, 면적 비율(ISTD 분석법), 높이 또는 높이 비율(ISTD 분석법)) 또는 양(양, 양 비율(ISTD 분석법)) |
및
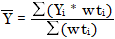
여기에서
| wti | 데이터 포인트의 가중치 |
| Ȳ | 예측된 감응 또는 양의 평균 값 |
| Yi | 예측된 감응 또는 양(결합된 검량 곡선 사용) |
강제된 원점의 경우 지점이 0을 중심으로 하며(세 번째 사분면으로 미러링됨) 평균 값이 0으로 치환된다고 가정합니다. 타사 계산 프로그램은 다른 접근 방식을 사용할 수 있으며, 이 경우 약간 다른 결과가 나올 수 있습니다.
상관 계수는 완벽하게 맞는 경우 1입니다. 개별 또는 평균 검량점이 회귀 곡선에서 벗어날수록 감소합니다. 일반적인 값은 0.99에서 1 사이입니다. 상관 계수는 분석법의 정밀도를 직접적으로 나타내는 척도는 아니지만 값이 낮으면 정밀도가 낮다는 것을 의미합니다.
결정 계수
결정 계수(R²)는 다음과 같이 계산됩니다.
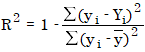
여기에서
| R² | 결정 계수 |
| ȳ | 측정된 감응 또는 양의 평균 값 결합된 검량 곡선이 원점을 강제로 통과하는 경우(처리 방법에서 원점=힘) OpenLab CDS는 중심이 없는 결정 계수를 계산합니다. 이 경우 ӯ는 생략됩니다. |
| yi | 측정된 감응 또는 양. 감응은 면적(면적, 면적% 또는 면적 비율(ISTD 분석법)) 또는 높이(높이, 높이% 또는 높이 비율(ISTD 분석법))일 수 있습니다. 양은 절대 양 또는 양 비율(ISTD 분석법)일 수 있습니다. 값 유형은 검량 모드에 따라 다릅니다. |
| Yi | 예측된 감응 또는 양(결합된 검량 곡선 사용) |
잔차 표준 편차
잔차 표준 편차(평균제곱근 오차라고도 함)는 다음 공식을 사용하여 계산합니다.
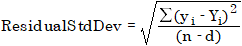
위치
d = 3 | 이차 곡선의 자유도, 강제된 원점 없음 |
d = 2 | 강제된 원점이 있는 이차 곡선의 자유도 또는 선형 곡선의 자유도, 강제된 원점 없음 |
d = 1 | 강제된 원점이 있는 선형 곡선의 자유도 |
ResidualStdDev | 잔차 표준 편차 |
yi | 검량 모드에 따라 측정된 감응(면적, 면적 비율(ISTD 분석법), 높이 또는 높이 비율(ISTD 분석법)) 또는 양(양, 양 비율(ISTD 분석법)) |
Yi | 예측된 감응 또는 양(결합된 검량 곡선 사용) |
n | 검량점 수 |
원점 포함 결합된 검량 곡선 유형의 경우, 원점(0,0)이 계산에 정규 지점으로 포함되며 n으로 계산됩니다.
y값에는 가중치가 적용되지 않습니다.
잔차 표준 편차는 상관 계수보다 곡선 품질을 더 민감하게 측정할 수 있습니다. 완벽하게 맞는 경우 잔차 표준 편차는 0입니다. 잔차 표준 편차 값이 증가하면 검량점이 곡선에서 더 멀어집니다.
표준 편차
표준 편차는 모표준 편차 공식을 사용하여 계산합니다:
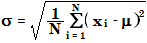
위치
σ | 표준 편차 |
N | 시료 수 |
xi | 측정값 감응 또는 양입니다. 곡선 모델 평균 RF의 경우, 단일 시료에서 화합물의 감응 계수 RF입니다. |
μ | 평균 값. 곡선 모델 평균 RF의 경우, 모든 시료에서 화합물의 평균 감응 계수입니다. |
참고
곡선 모델 평균 RF의 경우: 일반적으로 모집단(검량점 수)이 다소 작기 때문에 표본 모집단 표준편차(분모는 N-1) 대신 이 공식이 사용됩니다.
상대 표준 편차
상대 표준 편차는 다음과 같이 계산됩니다.
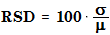
위치
RSD | 상대 표준 편차 |
σ | 표준 편차 |
μ | 평균값 |
base-id: 11016668427
id: 11016668427