Estatísticas da curva de calibração

O cálculo da curva de calibração fornece para cada curva os números do coeficiente de correlação, coeficiente de determinação e desvio padrão residual.

Coeficiente de correlação

O coeficiente de correlação (r) dá uma medida do ajuste da curva de calibração entre os pontos de dados. É calculado utilizando a seguinte equação:

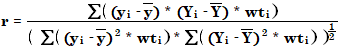
onde

	r	Coeficiente de correlação
	p_i	Peso do ponto de dados
	ӯ	Valores médios das respostas ou quantidades medidas Se a curva de calibração for forçada através da origem (Origem=Força no método de processamento), o OpenLab CDS calcula o coeficiente de determinação não centrado. Neste caso, ӯ é omitido.
	yi	Resposta medida (Área, ProporçãoÁrea (método ISTD), Altura ou ProporçãoAltura (método ISTD)) ou quantidade (Quantidade, ProporçãoQuantidade (método ISTD)), dependendo do modo de calibração
		Valores médios das respostas ou quantidades previstas
	Yi	Resposta ou quantidade prevista (usando a curva de calibração)

e são valores médios das respostas ou quantidades medidas e previstas, calculados da seguinte forma:

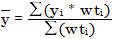
onde

	p_i	Peso do ponto de dados
		Valores médios das respostas ou quantidades medidas
	yi	Resposta medida (Área, ProporçãoÁrea (método ISTD), Altura ou ProporçãoAltura (método ISTD)) ou quantidade (Quantidade, ProporçãoQuantidade (método ISTD)), dependendo do modo de calibração

e

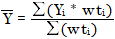
onde

	p_i	Peso do ponto de dados
		Valores médios das respostas ou quantidades previstas
	Yi	Resposta ou quantidade prevista (usando a curva de calibração)

Para Origem Forçada presume-se que os pontos estejam centralizados em zero (refletidos no terceiro quadrante) e que os valores médios sejam substituídos por zero. Os programas de cálculos de terceiros podem usar uma abordagem diferente, o que gerará resultados ligeiramente diferentes.

O coeficiente de correlação é 1 para um ajuste perfeito. Reduz-se à medida que os pontos individuais ou médios de calibração se desviam da curva de regressão. Os valores típicos estão entre 0,99 e 1. O coeficiente de correlação não é uma medida direta de precisão do método analítico, mas valores baixos indicam baixa precisão.

Coeficiente de determinação

O coeficiente de determinação (R²) é calculado conforme segue:

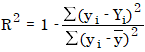
onde

	R2	Coeficiente de determinação
		Valores médios das respostas ou quantidades medidas Se a curva de calibração for forçada através da origem (Origem=Força no método de processamento), o OpenLab CDS calcula o coeficiente de determinação não centrado. Neste caso, ӯ é omitido.
	yi	Resposta ou quantidade medida. A resposta pode ser área (Área, Área% ou ProporçãoÁrea [método ISTD]) ou altura (Altura, Altura% ou ProporçãoAltura [método ISTD]). A quantidade pode ser quantidade absoluta ou ProporçãoQuantidade (método ISTD). O tipo do valor depende do modo de calibração.
	Yi	Resposta ou quantidade prevista (usando a curva de calibração)

Desvio padrão residual

O desvio padrão residual (às vezes denominado erro de raiz quadrada média) é calculado utilizando a seguinte fórmula:

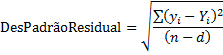
onde
d = 3	Grau de liberdade para uma curva quadrática, sem origem forçada
d = 2	Grau de liberdade para uma curva quadrática com origem forçada, ou Grau de liberdade para uma curva linear, sem origem forçada
d = 1	Grau de liberdade para uma curva linear com origem forçada
DesPadrãoResidual	Desvio padrão residual
yi	Resposta medida (Área, ProporçãoÁrea (método ISTD), Altura ou ProporçãoAltura (método ISTD)) ou quantidade (Quantidade, ProporçãoQuantidade (método ISTD)), dependendo do modo de calibração
Yi	Resposta ou quantidade prevista (usando a curva de calibração)
n	número de pontos de calibração

Para curvas de calibração com opção de Incluir origem, a origem (0,0) é incluída como um ponto regular no cálculo e contada por n.

Os valores de y não são ponderados.

O desvio padrão residual proporciona uma medida mais sensível da qualidade da curva que o coeficiente de correlação. Para um ajuste perfeito, o desvio padrão residual é zero. Com o aumento dos valores do desvio padrão residual, os pontos de calibração ficam mais longe da curva.

Desvio padrão

O desvio padrão é calculado com a fórmula para desvio padrão de população:

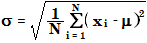
onde
σ	Desvio padrão
N	Número de amostras
x_i	Resposta ou quantidade de valor medida. Para o RF médio de modelo de curva, esse é o fator de resposta de um composto em uma amostra única..
μ	Valor médio. Para o RF médio de modelo de curva, esse é o fator de resposta médio de um composto em todas as amostras.

Para o modelo de curva RF médio: Devido à população normalmente pequena relativamente (número de pontos de calibração), esta fórmula é usada em vez do desvio padrão de população da amostra (com N-1 como denominador).

Desvio padrão relativo

O desvio padrão relativo é calculado da seguinte forma:

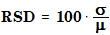
onde
RSD	Desvio padrão relativo
σ	Desvio padrão
μ	Valor médio

PVCS#B-02561