校正曲线统计
校正曲线计算为各个曲线提供了相关系数、确定系数和残余标准差。
相关系数
相关系数 (r) 是对不同数据点之间校正曲线的拟和实测。其计算公式如下:
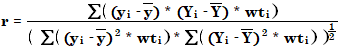
其中
| r | 相关系数 |
| wti | 数据点的加权 |
| ӯ | 测量的响应值或含量的平均值 如果校正曲线强制通过原点(处理方法中的原点=强制),则 OpenLab CDS 会计算未居中的确定系数。在这种情况下,将会忽略 ӯ。 |
| yi | 测量的响应值(峰面积、峰面积比率(内标方法)、峰高或峰高比率(内标方法))或含量,取决于校正模式 |
| Ȳ | 预测的响应值或含量的平均值 |
| Yi | 预测响应值或含量(使用校正曲线) |
ȳ 和 Ȳ 是测量和预测的响应值或含量的平均值,计算方法如下:
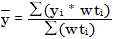
其中
| wti | 数据点的加权 |
| ȳ | 测量的响应值或含量的平均值 |
| yi | 测量的响应值(峰面积、峰面积比率(内标方法)、峰高或峰高比率(内标方法))或含量,取决于校正模式 |
和
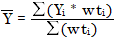
其中
| wti | 数据点的加权 |
| Ȳ | 预测的响应值或含量的平均值 |
| Yi | 预测响应值或含量(使用校正曲线) |
强制原点是假设点以零为中心(相对第三象限对称)且平均值可替换为零。第三方计算程序可能使用其他方法,结果可能会略有差异。
完全拟合的相关系数为 1。当单个或平均校正点偏离回归曲线时,其会减小。通常值在 0.99 和 1 之间。相关系数不是分析方法精度的直接衡量标准,但是值越低表明精度越低。
确定系数
确定系数 (R²) 计算方法如下:
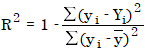
其中
| R² | 确定系数 |
| ȳ | 测量的响应值或含量的平均值 如果校正曲线强制通过原点(处理方法中的原点=强制),则 OpenLab CDS 会计算未居中的确定系数。在这种情况下,将会忽略 ӯ。 |
| yi | 测量的响应值或含量。响应值可以是峰面积(峰面积、峰面积% 或面积比率(内标方法))或峰高(峰高、峰高%或峰高比率(内标方法))。含量可以是绝对含量或含量比率(内标方法)。值的类型取决于校正模式。 |
| Yi | 预测响应值或含量(使用校正曲线) |
残留标准偏差
残留标准偏差(有时称为根均方差)计算公式如下:
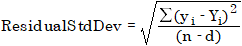
其中
d = 3 | 二次曲线的自由度,不强制过原点 |
d = 2 | 二次曲线的自由度,强制过原点,或 线性曲线的自由度,不强制过原点 |
d = 1 | 线性曲线的自由度,强制过原点 |
ResidualStdDev | 残留标准偏差 |
yi | 测量的响应值(峰面积、峰面积比率(内标方法)、峰高或峰高比率(内标方法))或含量,取决于校正模式 |
Yi | 预测响应值或含量(使用校正曲线) |
n | 校正点数量 |
对于包含原点的校正曲线类型,原点 (0,0) 作为计算中使用的常规点并计入 n。
y 值不加权。
与相关系数相比,残留标准偏差对曲线质量更为敏感。完全拟合的残留标准偏差为零。残留标准偏差越高校正点离曲线越远。
标准偏差
标准偏差用群体标准偏差的公式计算:
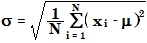
其中
σ | 标准偏差 |
N | 样品数目 |
xi | 测量响应值或含量。对于曲线模型平均 RF,它是单个样品中化合物的响应因子 RF。 |
μ | 平均值。对于曲线模型平均 RF,它是所有样品中化合物的平均响应因子。 |
注意
对于曲线模型平均 RF:由于正常情况下群体(校正点数)相当小,因此使用此公式来替代样品群体标准偏差(使用 N-1 作为分母)。
相对标准偏差
相对标准偏差的计算方式如下:
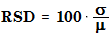
其中
RSD | 相对标准偏差 |
σ | 标准偏差 |
μ | 平均值 |
base-id: 11016668427
id: 11016668427