일반적인 접근 방식

 

전제 사항

모든 평활화 알고리즘은 데이터가 등거리 데이터라고 가정합니다. 등거리가 아닌 데이터는 보간을 적용하고 등거리가 아닌 데이터에서 가장 작은 시간차를 사용하여 데이터를 다시 샘플링하여 등거리 데이터로 변환됩니다.

비 MS 데이터는 스플라인 보간을 사용하여 변환됩니다.

MS 데이터의 경우 변환은 평활화 알고리즘에 따라 달라집니다. Savitzy-Golay에서는 스플라인 보간이 사용됩니다. 이동 평균 또는 가우시안에서는 선형 보간법이 사용됩니다.

평활화 - 기본 알고리즘

모든 평활화 알고리즘은 다음과 같은 접근 방식을 사용하여 평활화 계수로 채워진 2m+1 크기의 창을 적용합니다.

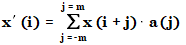
위치

a	평활 계수의 배열
x'	평활화된 신호
m	평활화 창의 절반 너비를 지정하는 짝수

이 방식을 사용하면 전체 창 크기가 홀수 2m+1가 됩니다.

가장자리 처리

평활 계수는 정규화되어야 하므로 가장자리를 특별히 고려해야 합니다.

이동 평균 및 가우시안 필터링의 경우, 창은 왼쪽 또는 오른쪽 가장자리에서 잘리고 계수는 총 합이 1이 되도록 다시 계산됩니다(정규화).

Savitzy-Golay의 경우 처리가 더 복잡합니다. 신호의 가장자리에 가까운 곳에서도 Savitzy-Golay 필터링의 특성을 보존해야 합니다. 알고리즘 세부 정보를 참조하십시오.